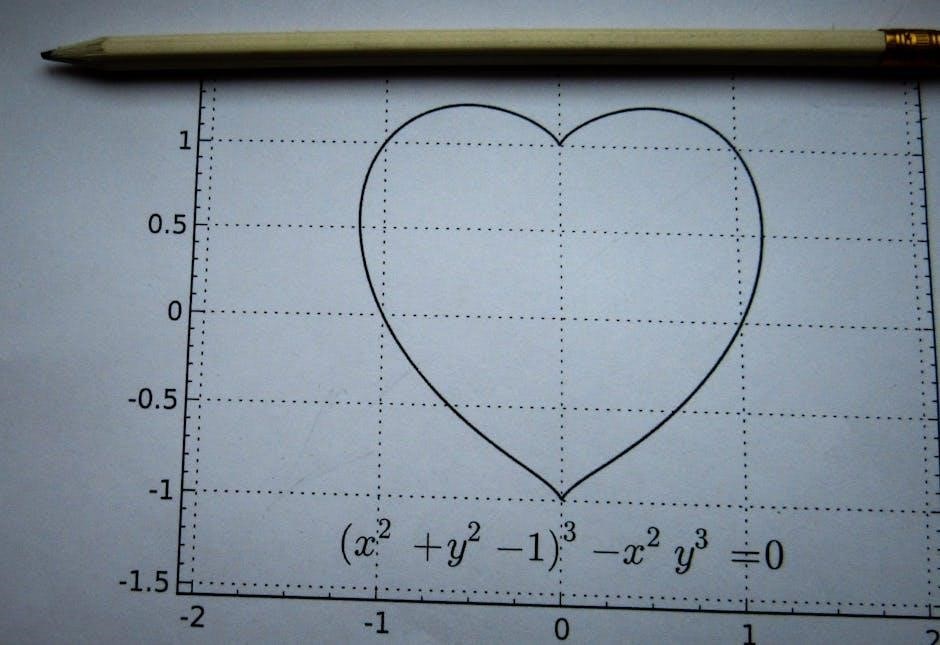
Pre-calculus bridges algebra and calculus‚ focusing on functions‚ trigonometry‚ and advanced math concepts. It prepares students for calculus by strengthening foundational skills and problem-solving abilities.
1.1 What is Pre-Calculus?
Pre-calculus is a foundational mathematics course designed to prepare students for calculus. It bridges the gap between algebra and calculus‚ focusing on advanced algebraic concepts‚ trigonometry‚ and functions. The curriculum typically includes topics such as polynomial and rational functions‚ exponential and logarithmic functions‚ trigonometric identities‚ and conic sections. Pre-calculus emphasizes problem-solving strategies‚ critical thinking‚ and the development of mathematical intuition. It is essential for students aiming to pursue higher-level mathematics‚ science‚ or engineering. By mastering pre-calculus‚ students build a robust foundation for understanding calculus concepts and applying them in real-world scenarios. Resources like textbooks and online materials‚ such as “Precalculus / Robert Blitzer‚” provide comprehensive guidance for learners.
1.2 Importance of Pre-Calculus in Mathematics
Pre-calculus is crucial as it bridges the gap between algebra and calculus‚ ensuring students are well-prepared for advanced mathematics. It builds a strong foundation in problem-solving‚ critical thinking‚ and mathematical intuition. By mastering pre-calculus‚ students gain the skills necessary to tackle complex concepts in calculus‚ physics‚ and engineering. The course emphasizes understanding functions‚ trigonometric identities‚ and conic sections‚ which are essential for STEM fields. Additionally‚ pre-calculus fosters analytical reasoning and logical thinking‚ skills that are valuable in many academic and professional settings. Without a solid grasp of pre-calculus‚ students may struggle with higher-level math‚ making it a vital stepping stone in their educational journey.
1.3 Overview of Pre-Calculus Topics
Pre-calculus curriculum covers a wide range of topics designed to prepare students for calculus and advanced mathematics. Key areas include functions and their properties‚ such as domain‚ range‚ and composition. Trigonometry is central‚ focusing on angles‚ identities‚ and applications. Polynomial and rational functions are explored in depth‚ along with exponential and logarithmic functions‚ which are essential for understanding growth and decay. Conic sections introduce geometric concepts‚ while sequences and series lay the groundwork for calculus. The course also emphasizes problem-solving strategies and the use of graphs to visualize and analyze mathematical relationships. Together‚ these topics build a comprehensive foundation‚ ensuring students are equipped for the challenges of higher-level math.

Key Topics in Pre-Calculus
Pre-calculus focuses on functions‚ trigonometry‚ conic sections‚ polynomials‚ rational functions‚ exponential and logarithmic functions‚ and sequences and series‚ building foundational math skills for advanced studies.
2.1 Functions and Their Properties
Functions are a cornerstone of pre-calculus‚ representing relationships between variables. Key properties include domain‚ range‚ and composition. Understanding function transformations‚ such as shifts and scaling‚ is crucial. Inverse functions and their properties are also explored‚ along with even and odd functions. The study of function behavior‚ including continuity and end behavior‚ prepares students for advanced calculus concepts. Practical applications of functions in real-world scenarios‚ such as modeling growth and change‚ emphasize their importance. Mastery of function properties ensures a solid foundation for analyzing polynomial‚ rational‚ exponential‚ and logarithmic functions later in the course.
2;2 Trigonometry Basics
Trigonometry‚ a fundamental component of pre-calculus‚ focuses on the relationships between angles and side lengths of triangles. It introduces core concepts like sine‚ cosine‚ and tangent functions‚ which describe ratios in right triangles. Students explore trigonometric identities‚ including the Pythagorean identity‚ and learn to solve equations involving these functions. Understanding angle measures‚ such as degrees and radians‚ is essential. The unit circle is also introduced‚ providing a framework for analyzing periodic behavior. Trigonometric functions are graphed to visualize their periodicity and amplitude. Mastery of these basics is critical for solving real-world problems‚ such as determining heights or distances‚ and for advancing to calculus topics like circular motion and wave analysis.
2.3 Conic Sections
Conic sections are geometric figures formed by the intersection of a plane with a double-napped cone. They include circles‚ ellipses‚ parabolas‚ and hyperbolas. In pre-calculus‚ students learn to analyze and graph these shapes by deriving their equations. The standard forms of conic sections are introduced‚ such as the equation of a circle (x-h)² + (y-k)² = r² and the ellipse equation (x-h)²/a² + (y-k)²/b² = 1. Understanding conic sections involves identifying key features like foci‚ vertices‚ and asymptotes. These concepts are essential for solving problems in physics‚ engineering‚ and astronomy. Graphing conic sections helps visualize their properties and prepares students for advanced calculus topics involving parametric equations and polar coordinates.
2.4 Polynomial and Rational Functions
Polynomial and rational functions are central to pre-calculus‚ building on algebraic concepts. Polynomials are expressions of the form P(x) = a_nx^n + … + a_1x + a_0‚ where n is the degree. They are classified as linear‚ quadratic‚ cubic‚ or higher‚ each with distinct graph shapes. Rational functions involve ratios of polynomials‚ such as f(x) = P(x)/Q(x)‚ and are analyzed for asymptotes‚ holes‚ and intercepts. Understanding these functions is crucial for solving equations‚ modeling real-world phenomena‚ and transitioning to calculus. Polynomial functions are continuous and smooth‚ while rational functions can have discontinuities. Both are essential for advanced problem-solving in mathematics and science.
2.5 Exponential and Logarithmic Functions
Exponential and logarithmic functions are fundamental in pre-calculus‚ essential for modeling growth‚ decay‚ and inverses. Exponential functions follow the form y = ab^x‚ where a and b are constants‚ with b > 0 and b ≠ 1. When b > 1‚ the function grows rapidly‚ and when 0 < b < 1‚ it decays. Logarithmic functions‚ the inverse of exponentials‚ are represented as y = log_b(x)‚ answering: "To what power must b be raised to obtain x?" Key properties include log_b(xy) = log_b(x) + log_b(y) and log_b(x^n) = n log_b(x)‚ aiding in simplifying expressions and solving equations.
Graphing these functions reveals distinct behaviors: exponentials have horizontal asymptotes‚ while logarithmics have vertical asymptotes. Solving exponential and logarithmic equations often involves taking logarithms of both sides. Real-world applications include population growth and sound measurement‚ showcasing their versatility and importance in various fields.
2.6 Sequences and Series
Sequences and series are essential concepts in pre-calculus‚ introducing students to the study of ordered lists of numbers and their summation. A sequence is a set of numbers arranged in a specific order‚ such as arithmetic or geometric sequences. An arithmetic sequence has a constant difference between terms‚ while a geometric sequence has a constant ratio. Series‚ on the other hand‚ represent the sum of the terms in a sequence. Understanding sequences and series involves mastering formulas for the nth term‚ partial sums‚ and the concept of convergence for infinite series. These topics lay the groundwork for calculus‚ particularly in limit and integral concepts‚ and are crucial for solving problems in fields like finance and physics. They also enhance problem-solving skills and mathematical reasoning‚ emphasizing pattern recognition and the application of properties to real-world scenarios.

Resources for Pre-Calculus Study
Textbooks like Barrons Math 360: Pre-Calculus and Precalculus by Robert Blitzer are excellent resources. Online platforms‚ practice worksheets‚ and video tutorials provide comprehensive support for mastering pre-calculus concepts effectively.
3.1 Best Pre-Calculus Textbooks
Some of the most recommended pre-calculus textbooks include Barrons Math 360: Pre-Calculus and Precalculus by Robert Blitzer. These textbooks provide comprehensive coverage of essential topics like functions‚ trigonometry‚ and conic sections. They are designed to build a strong foundation for calculus and include practice problems‚ examples‚ and detailed explanations. Blitzer’s text‚ for instance‚ is known for its clear presentation and relevance to real-world applications. Additionally‚ some textbooks offer advanced content bridging pre-calculus and calculus‚ making them ideal for students aiming to transition smoothly. These resources are widely used in classrooms and are highly regarded for their clarity and effectiveness in teaching complex mathematical concepts.
3.2 Online Resources and Websites
Online resources like Khan Academy and MIT OpenCourseWare offer free pre-calculus materials‚ including video lectures and practice problems. Websites such as Mathway provide step-by-step solutions to equations‚ aiding homework completion. Desmos is another valuable tool‚ offering an interactive graphing calculator for visualizing functions and conic sections. Additionally‚ platforms like Coursera and edX host pre-calculus courses from top universities‚ suitable for self-paced learning. These resources complement textbooks and classroom instruction‚ helping students master concepts through diverse learning methods. They also cater to different learning styles‚ ensuring that students can grasp complex topics at their own pace and convenience.
3.3 Practice Problems and Worksheets
Practice problems and worksheets are essential for mastering pre-calculus concepts. Websites like Khan Academy and Mathway offer interactive exercises and step-by-step solutions. PDF worksheets from educational platforms provide targeted practice on topics such as functions‚ trigonometry‚ and polynomial equations; Many textbooks‚ like Barron’s Math 360‚ include companion worksheets for reinforcement. These resources allow students to test their understanding‚ identify weaknesses‚ and improve problem-solving skills. Additionally‚ online platforms often categorize problems by difficulty‚ making it easier to progress from basic to advanced topics. Regular practice with these materials ensures a solid grasp of pre-calculus fundamentals.
3.4 Video Tutorials and Lectures
Video tutorials and lectures are invaluable for visual learners studying pre-calculus. Platforms like Coursera and edX offer free courses with video lectures from universities like MIT and Stanford. YouTube channels such as 3Blue1Brown and Crash Course provide engaging explanations of complex topics. These resources often include animations and real-world examples‚ making abstract concepts easier to understand. Additionally‚ many pre-calculus textbooks‚ like Barron’s Math 360‚ offer companion video lectures. Students can pause‚ rewind‚ and revisit lessons‚ allowing for self-paced learning. Video tutorials also cover specific skills‚ such as trigonometric identities or function transformations‚ making them ideal for targeted practice and review.
Study Tips for Pre-Calculus
Mastering pre-calculus requires consistent practice‚ understanding foundational concepts‚ and seeking help when needed. Regular review and applying concepts to real-world problems enhance comprehension and retention effectively.
4.1 Building a Strong Foundation
Building a strong foundation in pre-calculus is essential for success in higher-level mathematics. This involves mastering core concepts such as functions‚ trigonometry‚ and algebraic manipulations. Students should focus on understanding the underlying principles rather than memorizing formulas. Consistent practice and regular review of topics like graphing‚ equations‚ and inequalities are crucial. Additionally‚ leveraging resources such as textbooks‚ online tutorials‚ and practice worksheets can reinforce learning. By dedicating time to these areas‚ students create a solid base that will support their progress in calculus and beyond.
4.2 Effective Practice Strategies
Effective practice strategies are vital for excelling in pre-calculus. Set specific goals for each study session and focus on active learning techniques‚ such as solving problems step-by-step. Utilize online resources and video tutorials to supplement textbook learning. Regular practice‚ even for short durations‚ helps reinforce concepts. Review mistakes thoroughly to avoid repeating them. Incorporate technology‚ like graphing calculators or math apps‚ to visualize problems and explore solutions dynamically. Collaborate with peers or join study groups to discuss challenging topics. Consistency and dedication are key to mastering pre-calculus‚ ensuring a smooth transition to more advanced mathematics.
4.3 Seeking Help and Resources
Seeking help and utilizing available resources is crucial for success in pre-calculus. Don’t hesitate to ask questions early to avoid misunderstandings. Textbooks like Barrons Math 360 offer comprehensive guides‚ while online platforms provide video tutorials and practice problems. Websites like Khan Academy and textbooks such as Precalculus by Robert Blitzer are excellent for supplementary learning. Join study groups or forums to discuss challenging topics with peers. Additionally‚ many educators provide free‚ peer-reviewed resources that align with course requirements. Use search tools to find specific skills or topics‚ and leverage technology like graphing calculators for visualizing concepts. Consistent practice and seeking help when needed will build confidence and mastery in pre-calculus.

Common Challenges in Pre-Calculus
Pre-calculus presents challenges like understanding trigonometric concepts‚ mastering function transformations‚ solving complex equations‚ and keeping up with coursework‚ which requires strong algebraic skills and consistent practice.
5.1 Understanding Trigonometric Concepts
Trigonometric concepts are fundamental in pre-calculus‚ focusing on relationships between angles and side lengths in triangles. Students often struggle with memorizing identities and solving trigonometric equations. Mastering the unit circle‚ sine‚ cosine‚ and tangent functions is essential. Many find it challenging to apply trigonometric principles to real-world problems‚ such as determining heights or distances. Additionally‚ graphing trigonometric functions and understanding their periodic nature can be confusing. Building intuition through visual aids and practice helps overcome these challenges. Online resources and practice worksheets are highly recommended to reinforce these concepts and improve problem-solving skills.
5.2 Mastering Function Transformations
Function transformations are a critical area in pre-calculus‚ involving the manipulation of function graphs through shifting‚ stretching‚ compressing‚ and reflecting. Students often find it challenging to distinguish between vertical and horizontal transformations and to apply them correctly. Understanding how changes in the function’s equation alter its graph is essential. Common struggles include identifying the order of transformations and applying multiple transformations simultaneously. Visual aids‚ such as graphing calculators or software‚ can help students visualize these changes. Practice with worksheets and online resources is highly recommended to build intuition and mastery. Additionally‚ video tutorials and step-by-step explanations can clarify complex concepts‚ enabling students to apply transformations confidently in various mathematical scenarios.
5.3 Solving Complex Equations
Solving complex equations is a cornerstone of pre-calculus‚ requiring a deep understanding of algebraic manipulation and problem-solving strategies. These equations often involve multiple variables‚ higher-degree polynomials‚ and exponential or logarithmic components. Students frequently struggle with identifying the appropriate methods to simplify and solve these equations‚ such as factoring‚ substitution‚ or using properties of exponents and logs. Additionally‚ equations involving trigonometric identities can be particularly challenging‚ as they require a strong grasp of identity transformations. Utilizing online resources‚ practice worksheets‚ and video tutorials can provide students with the tools and practice needed to master these equations. Breaking down problems into manageable steps and cross-verifying solutions are effective strategies to build confidence and accuracy in solving complex equations.
5.4 Keeping Up with Coursework
Keeping up with pre-calculus coursework can be challenging due to the rapid introduction of new concepts and the cumulative nature of the material. Students often struggle with balancing the workload while maintaining understanding‚ especially as topics like functions‚ trigonometry‚ and conic sections build on one another. Procrastination can lead to falling behind‚ making it difficult to grasp subsequent lessons. To stay on track‚ creating a structured study schedule and dedicating regular time to review and practice is essential. Leveraging online resources‚ such as video tutorials and practice worksheets‚ can also help reinforce concepts and fill gaps in understanding. Consistent effort and seeking help early when struggling are key to managing the coursework effectively.

Transitioning to Calculus
Pre-calculus serves as a bridge to calculus‚ emphasizing functions‚ limits‚ and trigonometric concepts. It equips students with the foundational skills necessary for success in calculus studies.
6.1 Preparing for Calculus I
Pre-calculus is essential for building the skills needed for Calculus I. It focuses on functions‚ trigonometry‚ and logarithmic concepts‚ which are foundational for understanding limits and derivatives. Students should master function transformations‚ trigonometric identities‚ and exponential growth models. Practicing with graphs and solving complex equations will enhance problem-solving abilities. Additionally‚ reviewing sequences and series prepares students for summing infinite series in calculus. Utilizing pre-calculus textbooks and online resources can provide structured guidance. Regular practice with worksheets and video tutorials ensures a solid understanding of key topics‚ making the transition to calculus smoother and more manageable.
6.2 Bridging the Gap Between Pre-Calculus and Calculus
Pre-calculus serves as the critical link between algebra and calculus‚ equipping students with essential skills in functions‚ trigonometry‚ and logarithmic concepts. By mastering these areas‚ students build a robust foundation for understanding calculus principles such as limits‚ derivatives‚ and integrals. The study of function transformations‚ exponential growth models‚ and trigonometric identities in pre-calculus directly prepares students for analyzing rates of change and accumulations in calculus. Additionally‚ the emphasis on problem-solving strategies and graphical interpretations in pre-calculus fosters the analytical thinking required for calculus. Regular practice with sequences‚ series‚ and complex equations further reinforces the mathematical dexterity needed for advanced studies; Thus‚ pre-calculus not only bridges the gap but also accelerates the transition to calculus by aligning foundational concepts with future applications.
6.3 Essential Skills for Success in Calculus
Mastering pre-calculus concepts is crucial for excelling in calculus. Key skills include understanding functions‚ their transformations‚ and compositions‚ as well as trigonometric identities and exponential/logarithmic relationships. Proficiency in analyzing conic sections‚ polynomial operations‚ and sequences/series is also vital. Developing strong problem-solving strategies and the ability to interpret graphs enhances preparedness for calculus. Additionally‚ familiarity with limits‚ rates of change‚ and accumulation concepts bridges the gap between pre-calculus and calculus. Fluency in algebraic manipulations and logical reasoning further supports success in calculus. By solidifying these foundational skills‚ students can approach calculus with confidence and tackle advanced topics effectively.
Pre-calculus establishes a robust mathematical foundation‚ essential for advanced studies. Mastery of its concepts ensures readiness for calculus and future STEM pursuits‚ fostering academic and professional growth.
7.1 Recap of Key Concepts
Pre-calculus is a foundational course that prepares students for calculus by exploring essential mathematical concepts. Key topics include functions and their properties‚ trigonometric identities‚ conic sections‚ polynomial and rational functions‚ exponential and logarithmic functions‚ and sequences and series. These areas are crucial for building problem-solving skills and mathematical intuition. Understanding function transformations‚ trigonometric relationships‚ and advanced equation-solving techniques is particularly emphasized. Additionally‚ the course bridges algebraic and calculus-based thinking‚ ensuring students are well-prepared for higher-level math. Resources like textbooks and online tools provide comprehensive support for mastering these concepts. By grasping pre-calculus‚ students establish a solid foundation for success in calculus and beyond.
7.2 Final Tips for Mastery
To master pre-calculus‚ focus on consistent practice and understanding core concepts. Regularly review functions‚ trigonometry‚ and algebraic manipulations to build a strong foundation. Utilize textbooks and online resources like video tutorials and practice worksheets to reinforce learning. Seek help early when struggling with topics‚ as they often build on each other. Develop problem-solving strategies and learn to apply concepts to real-world scenarios. Stay organized and keep up with coursework to avoid falling behind. Most importantly‚ embrace challenges as opportunities to grow and deepen your mathematical intuition. With dedication and the right resources‚ you can confidently excel in pre-calculus and set yourself up for success in future math courses.
7.3 Encouragement for Further Study
Mastering pre-calculus is a significant achievement that opens doors to advanced mathematics and STEM fields. Embrace the challenge and recognize the value of persistence. As you progress‚ remember that each concept builds on the last‚ creating a strong foundation for calculus and beyond. Don’t be discouraged by setbacks—use them as opportunities to grow. Explore additional resources like textbooks‚ online tutorials‚ and practice worksheets to deepen your understanding. Stay curious and motivated‚ knowing that pre-calculus is a crucial step toward unlocking the power of mathematics. With dedication‚ you’ll not only excel in pre-calculus but also gain the confidence to tackle more complex topics in the future.